Apostilas sobre as geometrias não-euclidianas.

A gravura de Mauritius Escher, mostrada acima, serve maravilhosamente como ponto de partida para o relato que faço, a seguir, sobre as geometrias não-euclidianas. No curto espaço dessas apostilas é impossível fazer completa justiça ao trabalho e à imaginação dos matemáticos que anteviram, descreveram e explicaram as desconcertantes propriedades dessas geometrias alternativas. Espero apenas atiçar a curiosidade de vocês, meus leitores, e esperar que procurem, em textos mais sérios, a satisfação que esse tema costuma provocar em quem nele se aventura.
O quinto postulado dos Elementos de Euclides.
Cerca de 300 anos antes de Cristo, Alexandre da Macedônia fundou, no delta do rio Nilo, a cidade de Alexandria. Com uns trinta anos de fundada, Alexandria já tinha cerca de meio milhão de habitantes. Foi quando lá chegou um cidadão chamado Euclides, atraído pela já famosa biblioteca da cidade. E foi lá que ele escreveu um livro, os ELEMENTOS, tão importante na história da cultura humana quanto as obras de Homero, Platão e Aristóteles. Nesse livro, que foi, e ainda é, lido e estudado por toda a comunidade de matemáticos, Euclides desenvolve toda a estrutura da geometria e da teoria de números como era conhecida na época. E já no início do livro, após algumas definições e axiomas relacionados a objetos elementares como pontos, retas, círculos etc, Euclides apresenta cinco postulados fundamentais.
A palavra “postular” significa “pedir”. Portanto, postulados são pedidos para a gente aceite, independentemente de provas formais, uma determinada afirmação como sendo verdadeira. Sendo aceito, o postulado passa a ser usado para demonstrar outras afirmações menos básicas, os “teoremas”.
Os quatro primeiros postulados de Euclides são fáceis de aceitar. Eles dizem:
1) Por entre dois pontos é possível traçar uma reta.
2) Uma reta pode ser estendida indefinidamente para os dois lados.
3) Dado um centro e um raio, é sempre possível traçar um círculo.
4) Todos os ângulos retos são iguais entre si.
Ninguém implica com esses postulados pois eles são simples de entender e fáceis de aceitar. Não é assim com o quinto postulado que diz:
5) Se duas retas (A e B) em um plano são interceptadas por outra reta C tal que os ângulos (α e β) de um mesmo lado de C somam um valor menor que 180o, então as retas A e B, quando prolongadas do lado dos ângulos α e β, irão se encontrar em algum ponto.
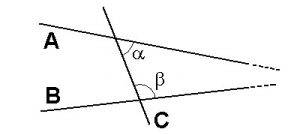
Os matemáticos, desde o início, acharam que esse postulado tinha cara de teorema. Isto é, talvez fosse possível demonstrá-lo usando os postulados anteriores e as definições básicas. Durante séculos, inúmeros matemáticos, alguns altamente competentes, tentaram achar uma demonstração para o Quinto Postulado, sempre sem sucesso. Em geral, quando alguém pensava que tinha “provado” o postulado, logo se descobria que a “demonstração” apenas trocava o enunciado original por outro equivalente. Por exemplo, o Quinto Postulado equivale a dizer que a soma dos ângulos de um triângulo é 180 graus. Portanto, provar o postulado usando esse fato não estará provando nada.
Nas próximas apostilas, vou contar em que deram essas tentativas de provar o Quinto Postulado de Euclides. Vocês vão ver que elas acabaram levando os matemáticos à surpreendente descoberta de que a geometria do velho Euclides não é a única possível.
As atribulações de padre Saccheri.
A vida do padre jesuíta Girolamo Saccheri (1667-1733) seria um prato cheio para os charlatães que escrevem livros de auto-ajuda se eles a conhecessem. O bom padre passou a vida perseguindo um objetivo: provar o Quinto Postulado dos Elementos de Euclides. Morreu decepcionado por não ter conseguido sucesso. E, no entanto, seu esforço não foi em vão pois suas pesquisas geométricas levaram, muitos anos depois, ao surgimento das geometrias não-euclidianas. No final, não conseguiu o que queria mas desvendou algo muito mais profundo.
Saccheri era um intelectual de primeira linha. Ensinou matemática, filosofia e, principalmente, teologia em várias universidades. Era também exímio enxadrista. Mas tinha, como objetivo primeiro na vida, provar o Quinto Postulado. Em 1733, ano de sua morte, publicou um livro intitulado “Euclides sem falhas: um trabalho que estabelece os princípios de uma geometria universal”. Esse título já dá a entender que Saccheri tinha perfeita noção do impacto de seu trabalho. Por outro lado, deixou para publicá-lo já no fim da vida, consciente de que estava apresentando alguma coisa muito avançada para seu tempo. Sua condição de jesuíta também não estimulava a defesa de teses revolucionárias. Como vamos ver a seguir, ele próprio chegou a duvidar do que estava demonstrando e evitou seguir a rota que desbravou até seu final grandioso.
O livro de Saccheri demonstra, corretamente, algumas dezenas de teoremas geométricos sempre com a intenção de, no final, demonstrar o Quinto Postulado. Para isso, ele usou uma variação equivalente do enunciado original.
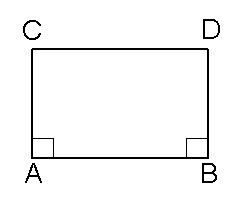
Imagine uma figura geométrica formada por quatro lados (um quadrilátero). Os ângulos da base, A e B, são retos e os segmentos AC e BD têm o mesmo comprimento.
Pois bem, o Quinto Postulado exige que o topo CD seja igual à base AB e que os ângulos C e D também sejam retos. Isto é, se Euclides estiver certo, essa figura tem de ser um retângulo. Portanto, para provar o Quinto Postulado basta provar que o quadrilátero de Saccheri é um retângulo.
Essa foi a missão que Saccheri encarou: provar que seu quadrilátero tinha de ser um retângulo. Saccheri gostava de usar um método de demonstração segundo o qual “negar a negação de uma proposição prova a proposição”. O próprio Euclides já usara esse método. No caso de seu quadrilátero, Saccheri contemplou 3 possibilidades:1) Caso OBTUSO: os ângulos C e D são maiores que 90°.
2) Caso EUCLIDIANO: os ângulos C e D são retos.
3) Caso AGUDO: os ângulos C e D são menores que 90°.
A esperança do jesuíta era conseguir mostrar que os casos OBTUSO e AGUDO levariam a contradições inaceitáveis e se reduziriam, pela força da lógica, ao caso EUCLIDIANO.
Levando avante esse projeto ele passou a demonstrar teoremas e mais teoremas, mas, para sua surpresa e frustração, não encontrava nenhuma falha lógica nos casos OBTUSO e AGUDO. Para ilustrar a situação em que ele se encontrou, vou mostrar a vocês alguns dos resultados que ele obteve. Veja, por exemplo, o segundo teorema do livro:
Teorema 2: “A linha EF que une o meio da base AB ao meio do topo CD do quadrilátero é perpendicular à base e ao topo.
O essencial, na prova desse teorema, é não usar a hipótese de que CD=AB, pois isso só vale no caso euclideano.
Temos, então, a seguinte seqüência de resultados: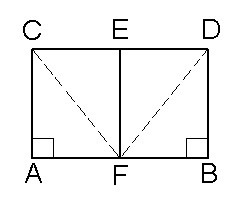
1) Construimos as linhas CF e DF.
2) O ângulo A é igual ao ângulo B, ambos ângulos retos, por construção. Logo, o triângulo CAF é igual ao triângulo DBF. Logo:
3) O triângulo CEF é igual ao triângulo DEF. Logo:
4) O ângulo CEF é igual ao ângulo DEF. Mas, a soma desses dois ângulos é 180°. Logo:
5) O ângulo CEF e o ângulo DEF valem, cada um, 90°. CQD
Como você deve ter notado, a hipótese de que CD = AB foi desnecessária para provar esse teorema. Isto é, ele vale sem precisar do Quinto Postulado. Portanto, vale para os três casos, OBTUSO, EUCLIDIANO E AGUDO.
Esse tipo de coisa se repete para todos os teoremas que Saccheri tenta e consegue demonstrar em seu livro. Logo no teorema seguinte ele mostra que:
Teorema 3: “O topo CD é MENOR que a base AB, no caso OBTUSO, IGUAL no caso EUCLIDIANO e MAIOR que ela, no caso AGUDO.
Não vou reproduzir aqui a demonstração desse teorema pois é um pouco longa. Mas, podem crer que ela não usa o Quinto Postulado nem tem nenhuma incoerência.
Mais adiante, em seu nono teorema, Saccheri chega a um resultado fundamental:
Teorema 9: “A soma dos ângulos de um triângulo é maior que 180o no caso OBTUSO, igual a 180° no caso EUCLIDIANO e menor que 180° no caso AGUDO”.
Essa demonstração é simples se usarmos o teorema 3. Vou mostrar apenas o caso AGUDO.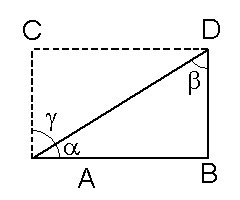
1) No caso AGUDO, CD > AB, como vimos no Teorema 3. Logo:
2) O ângulo g é MAIOR que o ângulo b. Logo:
3) α + β+ B < γ + α + B.
4) Como α + γ + B = 180°, por construção, temos:
5) α + β + B < 180°. CQD
Desse modo, Saccheri prosseguiu demonstrando seus teoremas sem nunca usar o Quinto Postulado e sem topar com nenhuma inconsistência nos casos AGUDO e OBTUSO. Para todos os efeitos, ele estava demonstrando que o Quinto Postulado só é imprescindível no caso EUCLIDIANO.
Por alguma razão, porém, Saccheri fraquejou. No seu Teorema 33 ele diz, meio desconcertado, que está demonstrando algo que “é contrário ao que se entende intuitivamente por linha reta”. Talvez por medo de estar cometendo algum engano só publicou seu livro no último ano de sua vida. Nunca soube que abrira as portas para outras geometrias até então desconhecidas.
Gauss, os Bolyai e Lobatchevski.
Carl Gauss, achava uma vergonha os matemáticos não conseguirem provar o Quinto Postulado. Ele próprio tentou um bocado e nunca conseguiu, embora achasse que o postulado talvez pudesse ser violado. Ele comentou isso com um amigo, Farkas Bolyai, também vítima da “quinta postulatite”, mania de querer provar ou desprovar o danado do postulado das paralelas.
Bolyai era natural da Transilvânia, portanto conterrâneo de Drácula e Frankenstein. Contou a seu filho, Janus Bolyai, a suspeita de Gauss. O filho era um rapaz talentoso e começou a trabalhar com o objetivo de comprovar o palpite de Gauss. Nisso, fez ouvido mouco às advertências do pai que lhe disse: “Pelo amor de Deus, esqueça isso. Essa mania é pior que a luxúria, vai acabar com sua paz de espírito e sua alegria de viver”. Mesmo assim Janus Bolyai não parou de trabalhar no assunto e logo começou a descobrir coisas interessantes. Por exemplo, ele constatou que, por um dado ponto, podia traçar um número infinito de retas paralelas a outra reta sem ferir nada que Euclides dissera em seu livro, a não ser, é claro, o Quinto Postulado. Em outras palavras: ele topara com uma geometria diferente da euclidiana mas tão coerente quanto ela. Entusiasmado, escreveu ao pai: “Criei um universo novo, tirando-o do nada”.
O velho Farkas logo informou, por carta a seu amigo Gauss, das proezas de seu rebento. E a resposta do grande Gauss foi uma ducha gelada: “Os resultados do trabalho de seu filho são excelentes mas, se eu elogiá-los estarei elogiando a mim mesmo, pois já os obtive há anos”. E acrescentou que não publicara suas descobertas por serem muito controversas e por não querer atiçar a fúria dos “beócios”.
Janus Bolyai ficou, evidentemente, muito decepcionado com essa resposta. E sua tristeza só aumentou quando soube que um russo chamado Nicolau Lobatchevski já tinha publicado resultados semelhantes dois anos antes. Como o artigo de Lobatchevski saiu em uma revista russa – e em russo – tinha passado despercebido pelo matemáticos europeus.
Essas disputas por precedência são comuns no mundo científico e, às vezes, resultam em injustiças. Quando você ouvir falar da “Lei de Fulano” ou do “Teorema de Sicrano”, pode desconfiar pois nem sempre eles são os verdadeiros autores. No caso que estamos tratando, acho que todos esses acima citados, Saccheri, Janus Bolyai, Gauss e Lobatchevski, são merecedores de nossa admiração e reverência. Além deles, que foram os pioneiros e desbravadores, outros vieram depois, como Riemann, Klein e Beltrami, que dotaram esse novo universo não-euclideano de uma estrutura lógica com todo o rigor matemático necessário. Disso falarei a seguir.
Riemann, Beltrami e as geometrias não-euclidianas.
No início do século 19 ainda não estava claro se o Quinto Postulado tinha validade absoluta ou se podia ser desobedecido em geometrias alternativas. Os trabalhos de Saccheri e Bolyai eram praticamente ignorados e as idéias de Lobatchevski eram tidas como absurdas por muitos matemáticos. Nessa época, o grande matemático alemão Bernhard Riemann chamou a atenção para uma falha cometida por Euclides, Saccheri e os outros pioneiros. É que eles sempre admitiam, sem contestar, que uma reta tem de ser infinita e ilimitada. Isso é dito no Segundo Postulado de Euclides e significa que, se um cidadão começasse a viajar em linha reta, seguindo a trajetória de um raio de luz, nunca chegaria ao fim da linha, mesmo se fosse eterno. Talvez isso valha apenas para o espaço euclideano e não seja necessário em outros espaços, sugeriu Riemann. Deixando de lado essa restrição, Riemann mostrou que podia criar uma geometria na qual a soma dos ângulos de um triângulo era MAIOR que 180 graus. Essa geometria corresponde perfeitamente ao caso OBTUSO de Saccheri.
Finalmente, em 1868, outro matemático italiano, Eugênio Beltrami, publicou um livro no qual, para todos os efeitos, fechou o ciclo dessas elocubrações. Nesse livro, chamado de “Ensaio sobre a interpretação de uma geometria não-euclidiana”, Beltrami descreve detalhadamente uma geometria perfeitamente lógica na qual a soma dos ângulos de um triângulo é MENOR que 180 graus. Com isso, obtinha o terceiro caso de Saccheri, o caso AGUDO.
Outros nomes mais descritivos foram então sugeridos para essas geometrias. São eles:
1) Geometria “elíptica”, do tipo descrita por Riemann e correspondente ao caso OBTUSO de Saccheri.
2) Geometria “plana”, correspondente à velha e boa geometria de Euclides.
3) Geometria “hiperbólica”, descrita por Lobatchevski e Beltrami e correspondente ao caso AGUDO de Saccheri.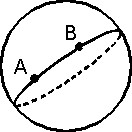
Os pioneiros não dispunham de modelos visuais para seus teoremas pois ainda estavam presos aos métodos de Euclides. Mas, com as sistematizações de Riemann e outros, ficou bem mais fácil para nós, humildes habitantes de um mundo aparentemente euclideano, enxergar de alguma forma como seriam essas outras geometrias.
A GEOMETRIA ELÍPTICA, que tem como caso particular a GEOMETRIA ESFÉRICA, pode ser visualizada pelo ponto de vista dos “chatóides” habitantes de um mundo de duas dimensões restrito à superfície de uma gigantesca esfera. Para esses chatóides, uma “reta”, isto é, a menor distância entre dois pontos, deve ser o segmento de um grande círculo que passa pelos pontos e cujo raio é o próprio raio da superfície esférica.
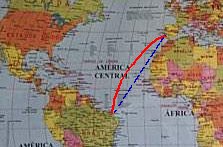
Hoje, com a rotina dos vôos internacionais, essa noção de “reta” ficou corriqueira. Um avião que vai de Fortaleza a Lisboa, sem escalas, não segue uma reta (em azul) traçada no mapa-mundi. Segue a trajetória (em vermelho) correspondente a um segmento de círculo máximo entre as duas cidades. Os chatóides e os pilotos concordam que essa é que é a “reta” real, pois é o caminho mais curto entre os dois pontos, seguindo a superfície terrestre.
Nessa geometria elíptica o Quinto Postulado de Euclides sofre um baque. Como uma “reta” é um círculo máximo somos levados às seguintes constatações surpreendentes.
1) Uma “reta” nessa geometria é ilimitada mas não é infinita. Um chatóide dessa geometria que saísse em linha reta seguindo a trajetória de um raio de luz acabaria, eventualmente, voltando ao ponto inicial, supondo que vivesse o tempo suficiente para toda a viagem. Foi essa a observação fundamental de Riemann, como contei acima.
2) Por um ponto P qualquer, fora de uma reta L, não passa nenhuma reta paralela a L!
Quer dizer, o Quinto Postulado é violado POR BAIXO. Isso é fácil de entender pois todos os círculos máximos de uma superfície esférica sempre se cruzam em pelo menos dois pontos.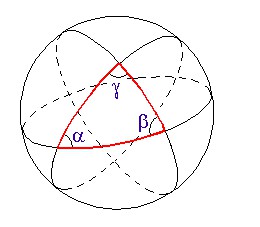
3) A soma dos ângulos de um triângulo na geometria elíptica é MAIOR que 180 graus.
Na figura,α + β+ γ > 180°.
Portanto, essa geometria corresponde ao caso OBTUSO do padre Saccheri. É notável lembrar que o esperto jesuíta intuiu esse resultado sem dispor desse tipo de visualização facilitadora criada, muito depois, por Riemann e outros.
Quem já leu minha apostila sobre a curvatura de Gauss, já sabe que esse espaço esférico tem curvatura positiva. Isso significa que esse tipo de espaço é encurvado para dentro, isto é, para o lado do raio da esfera.
Não preciso falar sobre a geometria PLANA pois ela corresponde à nossa familiar geometria euclidiana que todo estudante aprende na escola desde tempos remotos. Basta lembrar que nela o Quinto Postulado é obedecido sem problemas. E que tem CURVATURA NULA, isto é, o espaço é PLANO, não se encurva nem para dentro nem para fora em nenhum ponto.
A geometria HIPERBÓLICA, prevista inicialmente por Bolyai e Lobatchevski e desenvolvida por Beltrami, é a mais interessante das três, no meu modo de ver. Por isso, vou dedicar a ela toda a próxima apostila. Antes, quero só dizer que ela corresponde ao caso AGUDO de Saccheri e que tem curvatura negativa. Isto é, o espaço encurva-se para fora. A seguir, vou esclarecer melhor o que isso quer dizer.
A geometria hiperbólica e a pseudo-esfera.
Vimos, na apostila anterior, que a geometria elíptica pode ser visualizada, em duas dimensões, através da superfície de uma esfera (ou elipsóide) com curvatura positiva. A geometria hiperbólica, por sua vez, deve ser representada por uma superfície com curvatura negativa. Apesar do seu nome, as melhores escolhas para isso não envolvem uma hipérbole. 
Uma superfície que atende esse requisito é essa, vista na figura ao lado, que parece uma sela. Dá para ver que, em qualquer ponto dessa superfície, duas curvas se cruzam com curvaturas para lados opostos. Isso faz a curvatura de Gauss ser negativa, como já sabemos.

Beltrami usou outra superfície mais conveniente que a sela para representar a geometria hiperbólica. Ele chamou essa superfície de pseudo-esfera, por razões que logo ficarão evidentes, e mostrou que ela exibe as propriedades requeridas pela geometria hiperbólica de curvatura negativa. Isto é, em qualquer ponto da pseudo-esfera, do mesmo modo que na sela, curvas se cruzam com curvaturas em sentidos opostos. É possível ver isso na figura ao lado que mostra um modelo da pseudo-esfera.
Deixe-me explicar como se obtém essa superfície. Começamos traçando uma curva chamada “tractriz”, usando o seguinte procedimento.
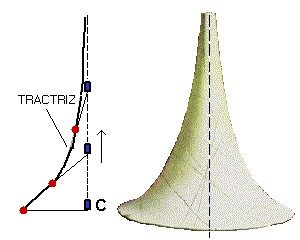
Imagine um carrinho C percorrento uma linha reta sobre o tampo de uma mesa. Na traseira do carrinho amarra-se um cordão bem esticado, inicialmente perpendicular à reta que o carrinho percorre. Na ponta desse cordão põe-se um pequeno disco que deixa um rastro pela mesa ao deslisar sobre ela. Pois bem, puxando-se o carrinho o rastro traçado pelo disco é uma tractriz, nome bem apropriado, portanto.
Depois, fazemos a tractriz girar em torno da reta pontilhada e obtemos uma superfície de revolução que é a pseudo-esfera que pode ser modelo para a geometria hiperbólica.
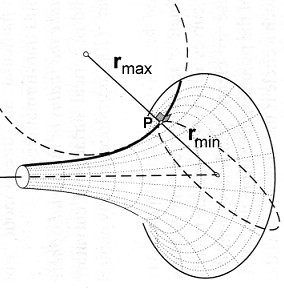
Definindo a curvatura local k como sendo o produto das curvaturas máxima e mínima em qualquer ponto da superfície é possível mostrar que, para a pseudo-esfera, k = – 1 / R², valor negativo, sendo R uma constante chamada de raio da pseudo-esfera. Os raios de curvatura máximo e mínimo em um dado ponto P são ilustrados na figura abaixo. Lembrando que, para a esfera, a curvatura é k = 1 / R², onde R é o raio da esfera, vemos que o nome “pseudo-esfera” para essa superfície usada por Beltrami é bem apropriado.
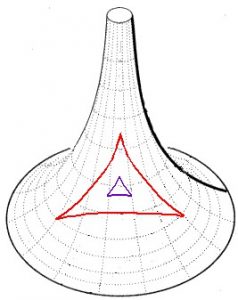
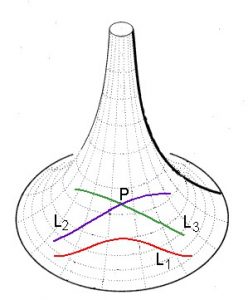
A soma dos ângulos de um triângulo desenhado sobre a superfície de uma pseudo-esfera é MENOR que 180 graus, como esperado de uma superfície que represente a geometria hiperbólica e o caso AGUDO de Saccheri. Observe que quanto maior o triângulo, menor é a soma de seus ângulos. Isso é exatamente o contrário do que se passa na geometria elíptica e na superfície da esfera que a representa. Além disso, por um ponto P podem passar infinitas “retas” paralelas a outra reta. Na figura, L2 e L3 são paralelas a L1 e se cruzam em um ponto P. Todas as “retas” que passam por P e estão entre L2 e L3 também são paralelas a L1. Dessa vez o Quinto Postulado é violado POR CIMA, coitado.
A pseudo-esfera de Beltrami é interessante mas não é a melhor maneira de se visualizar a geometria hiperbólica. Dois defeitos desagradáveis da pseudo-esfera são: a) as “retas” sobre ela nem sempre são infinitas como deveriam ser; b) existem círculos nela que não podem ser encolhidos até virarem pontos. Por sorte, existem outras formas mais convenientes de representar o plano hiperbólico que não têm esses defeitos. Na próxima apostila, vou mostrar uma delas que é muito interessante.
O disco de Poincaré e as gravuras de Escher.
O grande matemático francês Henri Poincaré inventou um “mapa” que é ótimo para nos ajudar a visualizar o plano hiperbólico. Como veremos também, esse mapa foi usado genialmente por Mauritius Escher em algumas de suas gravuras.
Um mapa é um desenho gráfico que se propõe a representar, sobre uma folha plana de papel, o que existe na realidade em uma região geográfica cheia de acidentes. Reproduzir a superfície de uma esfera, como o globo terrestre, em um papel plano implica necessariamente em distorções. Vamos ver que isso também ocorre no mapa que Poincaré imaginou para representar o plano hiperbólico.
O mapa de Poincaré é do tipo que os matemáticos chamam de “mapa conforme”. Nesse tipo de mapa, os ângulos são mantidos invariantes pela transformação. Isto é, se duas “retas” do espaço hiperbólico se cruzam e formam um ângulo qualquer, as representações dessas duas retas no mapa também se cruzam formando o mesmo ângulo.
Resumidamente, o mapa de Poincaré transporta todo um plano do espaço hiperbólico para dentro de um círculo, o “disco ∑”, também chamado de “disco de Poincaré”. As seguintes regras são seguidas nesse mapa:
1) Todo ponto do plano hiperbólico corresponde a um, e só um, ponto dentro do disco ∑.
2) Uma “reta” do plano hiperbólico corresponde a um segmento de círculo encerrado dentro do disco ∑, cujas pontas se aproximam perpendicularmente da borda desse disco.
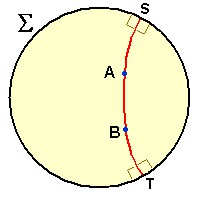
A figura mostra um disco ∑ como é visto por nós, habitantes de um espaço (supostamente) euclidiano e tri-dimensional. Todos os pontos de um plano do espaço hiperbólico foram obrigados a se acotovelarem dentro desse disco.
Por dois pontos quaisquer, A e B, passa uma – e só uma – “reta”. Dentro do disco ∑ essa “reta” tem a forma de um segmento de círculo cujas pontas são perpendiculares à borda do disco em S e T. Para todos os efeitos, esses pontos S e T nem existem propriamente, pois apenas simbolizam algo que está infinitamente distante no plano hiperbólico. Portanto, a “reta” que passa por A e B e que, para nós, parece ser curta e limitada, é, na verdade, infinita dos dois lados.
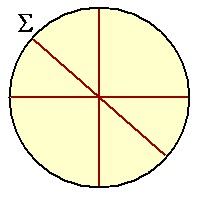
Existem “retas” do plano hiperbólico que, quando mapeadas no disco ∑ aparecem, para nós, como retas sem nenhum problema. Todas elas, é claro, têm de se encontrar no centro do disco ∑.
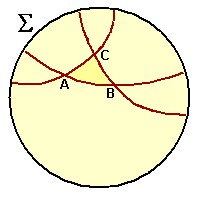
Três “retas” não colineares formam um triângulo ABC, como mostrado abaixo. A soma dos ângulos desse triângulo é MENOR que 180 graus, como requerido de uma representação correta do espaço hiperbólico. Lembrem que esses ângulos correspondem exatamente aos ângulos representados, já que a transformação é “conforme”. Na outra figura, vemos um triângulo reto no espaço hiperbólico representado no disco ∑.
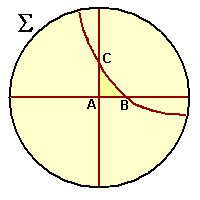
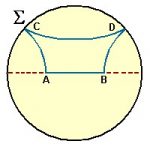
A figura ao lado mostra um quadrilátero de Saccheri representado no disco ∑. Tudo que o bom padre intuiu acerca de seu quadrilátero no caso AGUDO está presente nessa representação. A base AB é menor que o topo CD e os ângulos C e D são menores que 90 graus.
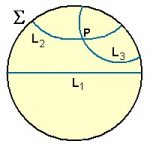
Usando essa representação fica fácil constatar que o Quinto Postulado de Euclides realmente não vale para o espaço hiperbólico. Na figura, temos uma “reta” L1 e um ponto P fora dela. Pode-se ver que as “retas” L2 e L3, que passam por P, nunca cruzam com a “reta” L1, logo, são paralelas a ela. Aliás, como vimos antes, podemos traçar um número infinito de “retas” paralelas a L1, todas se cruzando em P.
Brincar com o disco ∑ é uma diversão relaxante que recomendo a vocês. Um passatempo instrutivo, por exemplo, é procurar coisas que são verdadeiras no plano euclidiano mas não são no plano hiperbólico. Logo, não podem aparecer no disco ∑ de Poincaré. Vejam alguns exemplos que vocês podem confirmar.
1) Na geometria euclidiana dois triângulos podem ser semelhantes e não serem iguais em tamanho (ou “congruentes”, como dizem os geômetras). Isso é impossível na geometria hiperbólica, onde triângulos semelhantes têm de ser rigorosamente iguais.
2) A área de um triângulo euclidiano é dada por A = L H / 2, onde L é o comprimento da base e H é a altura. Isso não vale para triângulos hiperbólicos.
3) Na geometria hiperbólica não existem quadrados! Isto é, se um quadrilátero tiver 3 ângulos retos, o quarto não pode ser reto.
4) Um quadrilátero no espaço hiperbólico pode ter os quatro lados iguais e os quatro ângulos iguais, mas, todos os ângulos devem ser menores que 90 graus.
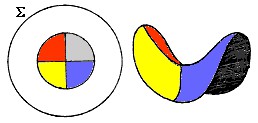
5) Se fosse possível cortar, com uma tesoura, um círculo que está dentro do disco ∑ e trazê-lo para nosso mundo euclidiano, ele imediatamente assumiria a forma de uma sela.
Se você prestar atenção, todas essas propriedades decorrem da não validade do Quinto Postulado na geometria hiperbólica.
Vamos ver agora como Mauritius Escher usou o disco ∑ em algumas de suas gravuras. Essas duas vistas abaixo são chamadas de Círculo Limite I (esquerda) e Círculo Limite III. Essa última, umas das poucas gravuras coloridas de Escher, foi feita em 1959.


Os peixes dessas gravuras são representações de nossos queridos “chatóides” (os “poincaretas”, se você preferir), habitantes do plano hiperbólico mapeado no disco ∑.
As gravuras mostram como nós, euclidianos impedernidos, vemos o mundo hiperbólico desses chatóides. Quando um chatóide se afasta do centro do disco, vemos seu tamanho encolher ficanto cada vez menor à medida que se aproxima do círculo limite. O chatóide, é claro, não concorda com essa nossa descrição do que acontece em seu mundo. Para ele, nada muda de tamanho quando se desloca pelo disco. Isso se justifica já que suas réguas e trenas são modificadas na mesma proporção que seus corpos.
Para nós, a velocidade de um raio de luz emitido pela lanterna de um chatóide também vai diminuindo quando se aproxima da periferia, além de seguir uma trajetória circular. O chatóide vê a luz seguir o que ele considera uma reta, com velocidade constante.
Por fim, para nós o universo dos chatóides parece finito. Para eles, é infinito: por mais que eles andem na direção do círculo limite nunca conseguem alcançá-lo.
Pronto. Agora já sabemos da existência das geometrias “elíptica” e “hiperbólica”, tão rigorosamente lógicas e respeitáveis quanto a milenar geometria euclidiana. A pergunta que provavelmente está em sua cabeça é: “qual é a geometria de nosso universo? Somos elípticos, euclidianos ou hiperbólicos”?
Vamos falar disso na próxima apostila.
Qual é a geometria do Universo?
Localmente, vivemos em um espaço euclidiano com 3 dimensões. Digo “localmente” porque, para efeitos de topografia, construção de prédios e orientação nas ruas a velha e boa geometria de Euclides funciona extremamente bem. Já em escalas maiores, com distâncias astronômicas, isso pode mudar. Para começar, a relatividade geral de Albert Einstein diz que a presença de matéria pode “encurvar” o espaço e modificar o tempo. Isto é, mesmo se nosso espaço for euclidiano quando vazio, perto de uma grande estrela ele se encurva e deixa de ser plano.
E, para complicar mais as coisas, os teóricos de supercordas acham 3 dimensões espaciais muito pouco e só conseguem fechar as complicadas contas que fazem com o uso de 10 ou mais dimensões. Bem, eu não entendo nada dessas modernidades e, por isso, não vou falar delas.
Volto, portanto, ao nosso familiar espaço 3D. Quando a NASA lança um feixe de luz laser na direção da Lua, por exemplo, os engenheiros fazem seus cálculos considerando que esse feixe seguiu uma reta bem retinha em um espaço tipicamente euclidiano. Mas será que essa reta é mesmo uma reta, ou será uma “reta”? Será que, do mesmo modo que os chatóides de Escher, somos “iludidos” por nossos sentidos adaptados à geometria do espaço onde vivemos? Um ser superpoderoso, habitante de um hipotético espaço de 4 dimensões (as nossas 3 e uma extra), observando o feixe de luz da NASA, o que veria? Será que concordaria com nossa visão de reta? Ou será que veria nosso feixe de luz seguir uma trajetória circular, como vimos acontecer com a luz dos chatóides habitantes do disco ∑? Nesse caso, ele diria que nós habitamos um mundo hiperbólico de 3 dimensões, a “esfera ∑”.
Será que dá para nós sabermos, independentemente de seres superpoderosos inexistentes, que tipo de espaço realmente habitamos?
Em princípio, deve dar. Se você leu minha apostila sobre a CURVATURA DE GAUSS, deve lembrar que bastaria a gente medir a soma dos ângulos de um triângulo de dimensões cosmológicas. Fácil de dizer, mas…
Mas, é mais ou menos isso que os cosmologistas estão tentando fazer. Na impossibilidade de fazer a experiência com a luz de seus tímidos lasers, eles usam a “luz” que vem dos confins do Universo para fazer seus testes de curvatura. Basicamente, eles querem saber se a curvatura global do Universo é positiva, como na geometria elíptica de Riemann, nula, como na geometria plana de Euclides ou negativa, como na geometria hiperbólica de Lobatchevski.
O que eles descobriram até agora é muito controverso. O caso é que, só muito recentemente, a cosmologia deixou de ser uma ciência puramente teórica e especulativa e passou a dispor de resultados observacionais confiáveis. Hoje, os cosmologistas estão recebendo dados obtidos em vários tipos de sondas e detetores, alguns na superfície da Terra e outros em órbita.
Talvez a melhor fonte de dados para esses testes de curvatura do Universo seja a famosa “radiação cósmica de fundo”. Que bicho é esse?
Logo que o Universo surgiu do Big Bang, sua temperatura era tão incrivelmente alta que ainda não dava para existir núcleos e átomos, só existia radiação. E ficou assim por uns 300.000 anos até que a temperatura atingiu um nível menos extravagante e a matéria nasceu da energia. Nesse “instante”, o Universo ficou “transparente” e a radiação remanescente começou a se espalhar por ele e continua se espalhando até hoje. Essa é a tal “radiação de fundo” e nenhuma luz que chega aos detetores dos astrofísicos pode ser mais antiga que essa. Ela andou um bocado de espaço e tempo até chegar aos detetores dos físicos e traz uma espécie de retrato do Universo quando jovem. A análise dessa radiação é a melhor forma de se investigar a geometria global de nosso Universo.
Só que, pelo menos por enquanto, nada está comprovado. O que já se sabe é que, desde sua fundação, o Universo se apresenta como extremamente homogêneo e isotrópico. “Homogêneo” significa que ele é do mesmo jeito em todos os pontos do espaço. Por exemplo, não existe uma região privilegiada onde haja muito mais matéria que a média do resto. E “isotrópico” quer dizer que todas as direções são equivalentes, isto é, o Universo tem a mesma cara para qualquer direção que se olhe. É claro que estamos nos referindo a coisas de dimensões cosmológicas, sem levar em conta miudezas como estrelas ou até mesmo galáxias.
Só com isso ainda não dá para decidir qual é a geometria do Universo. Há três possibilidades, cada uma associada a uma das três geometrias de que estamos falando desde o início desse relato. Se a geometria do Universo for “elíptica” ele tem curvatura global positiva. Nesse caso, a atual expansão do Universo eventualmente atingirá seu ápice e, a partir desse momento, o Universo passará a se contrair até o esmagamento total e completo. Se o Universo for “plano”, isto é, se for globalmente euclidiano, sua curvatura é zero e sua expansão vai diminuir com o tempo mas nunca cessará de todo. E, se a geometria do Universo for “hiperbólica”, a atual expansão não só prossegue como até aumenta de velocidade com o passar do tempo. Nesses dois últimos casos, o destino do Universo é a diluição final, a marcha inexorável para o vazio eterno.
As últimas notícias parecem indicar que o Universo é “plano” mas sua expansão está acelerando. Como isso é contraditório, os cosmologistas ficaram desconcertados e foram reler os artigos que Einstein escreveu por volta de 1915. Desses artigos eles recuperaram uma certa “constante cosmológica” que o próprio Einstein já tinha descartado como inútil. Essa “constante” é uma espécie de força misteriosa repulsiva que se contrapõe (se existir) à ação atrativa da gravidade. Einstein precisou inventá-la, originalmente, para evitar que suas equações descrevessem um Universo instável, fadado a só se contrair pela ação da gravidade. Por razões puramente filosóficas, herança de Aristóteles, Einstein teimava em supor que o Universo deveria ser “estático”, sem inchar nem murchar. Quando disseram a ele que o Universo não tinha nada de estático, pois estava se expandindo, ele abandonou sua “constante” como desnecessária. Agora, os cosmologistas acham que ela é muito necessária.
Para encurtar essa já muito longa conversa, o fato é que os cosmologistas estão confusos e desarvorados. Ainda não se sabe qual é a geometria do Universo. É possível que, com os equipamentos cada vez mais sensíveis que estão sendo construídos e postos em funcionamento, em breve surjam respostas mais precisas para todas essas questões. Eu, provavelmente, não estarei mais por aqui para ler sobre elas. Como já disse outras vezes, em breve poderei receber essas explicações por comunicação pessoal, direta da boca do acendedor do Big Bang. E se Ele não existir, pretendo reclamar no Decon mais próximo por ter sido vítima, desde criancinha, de propaganda enganosa.

